You watch a few movies on Netflix, and it starts to know your taste. It identifies the films that you will like and recommends accordingly! How does it know?
There are a lot of algorithms that can be used for Content recommendations. Although content providers like Netflix use much more sophisticated algorithms, we will explore a relatively simple but powerful approach known as Collaborative filtering.
Collaborative filtering
We will be using a neighborhood based item-item Collaborative Filtering.
consider a simplified system which has 3 users and 10 movies. Now a new user (Arthur) enters the system. Arthur has rated only 2 movies so far. Our goal is to recommend movies to Arthur. For simplicity, movie ratings in our system are integers between 1 and 5. The table below gives a snapshot of our system:
Ratings
| Movie 1 | Movie 2 | Movie 3 | Movie 4 | Movie 5 | Movie 6 | |
|---|---|---|---|---|---|---|
| Ford | 3 | 2 | 1 | 4 | 1 | 3 |
| Trillian | 2 | 2 | 5 | 5 | 0 | 2 |
| Zaphod | 5 | 4 | 3 | 2 | 4 | 1 |
| Arthur (new) | 5 | - | 2 | - | - | - |
Movies available
| Movie ID | Name | Genres |
|---|---|---|
| 1 | Toy Story | Animation, Children’s, Comedy |
| 2 | Toy Story 2 | Animation, Children’s, Comedy |
| 3 | Mad Love | Drama, Romance |
| 4 | 12 Angry Men | Drama |
| 5 | Jumanji | Animation, Children’s, Comedy |
| 6 | A Pyromaniac’s Love Story | Comedy, Romance |
Let’s move on. We want to recommend movies to Arthur. We will use a simple approach - predict the ratings Arthur will give to unseen movies. Then we can easily recommend movies by suggesting the highest rated movies that Arthur hasn’t seen yet. The basic idea of computing ratings is based on a notion of similarity. We need to find movies which are more/less similar based on the rating matrix given above.
Notation
R is an MxN rating matrix. Consequently, M denotes the total number of users, and N denotes the total number of movies.
Algorithm
Let’s define a similarity function. This is known as the cosine similarity function. It’s named so as it treats each movie (A column in the rating matrix) as a vector and computes the cosine distance between 2 given movies.
\(sim(M_p, M_q) = cos(\theta) = \cfrac{\vert \vec{M_p} \cdot \vec{M_q} \vert}{\vert \vec{M_p} \vert \cdot \vert \vec{M_q} \vert}\)
Here is the full version if you need to code it yourself:
\(sim(M_p, M_q) = \cfrac{\vert \sum_{i=1}^{M} R[i][M_p] \cdot R[i][M_q] \vert}{ \sqrt{\sum_{i=1}^{M} R[i][M_p]^2} \cdot \sqrt{\sum_{i=1}^{M} R[i][M_q]^2}}\)
Applying this similarity function, we get the following results:
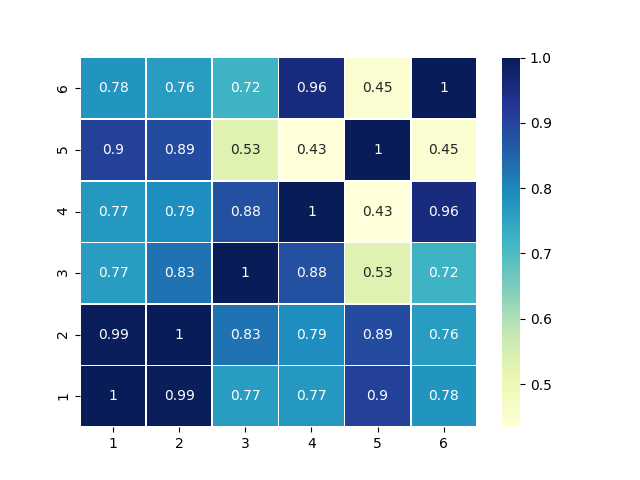
Now all the system needs to figure out is how to generate new ratings given this notion of how similarity.
Given a movie that Arthur hasn’t seen we take a weighted average of the movies with it’s neighbours and generate a rating.
(The default value for unseen ratings is defined as the average of all of Arthur’s ratings). \(R[U_i][M_j] = \cfrac{\sum_{k=1,k \neq j}^{M} sim(M_k,M_j) \cdot R[U_i][M_k] }{\sum_{k=1,k \neq j}^{M} sim(M_k,M_j)}\)
Thus when predicting ratings for a particular movie, ratings of similar movies have a greater impact on the predicted rating. That’s it!
Using the above formula, we get the following predictions
| Movie 1 | Movie 2 | Movie 3 | Movie 4 | Movie 5 | Movie 6 | |
|---|---|---|---|---|---|---|
| Arthur | 5 | 2.98 | 2 | 2.99 | 3.32 | 3.26 |
According to our reccomendation engine, Arthur should watch Movie 5 - Jumanji next.
Improvements
What we described was only a simple system. We can do much better by tweaking the above system to get better recommendations. In this section, I will demonstrate some of the improvements that I did, using the same example as above.
Biases
every person in the above database has some bias when they rate movies. In the example above, Zaphod tends to give out 4-5 star reviews easily while Trillian is much more conservative. To remove this bias, we subtract the average rating of a user while calculating the similarity function.
The updated function is as follows:
\(sim(M_p, M_q) = \cfrac{\sum_{i=1}^{M} (R[i][M_p]-\bar R_i) \cdot (R[i][M_q]-\bar R_i)}{ \sqrt{\sum_{i=1}^{M} (R[i][M_p]-\bar R_i)^2} \cdot \sqrt{\sum_{i=1}^{M} (R[i][M_1]-\bar R_i)^2}}\)
Similarly, while predicting the ratings, we predict how high/low the rating will be relative to the average. This has the advantage of producing zeros in the empty values (since we fill it with the average value).
\(R[U_i][M_j] = \bar R_i + \cfrac{\sum_{k=1,k \neq j}^{M} sim(M_k,M_j) \cdot (R[U_i][M_k]-\bar R_i) }{\sum_{k=1,k \neq j}^{M} sim(M_k,M_j)}\)
Let us see the correlation between the movies and our new predictions.
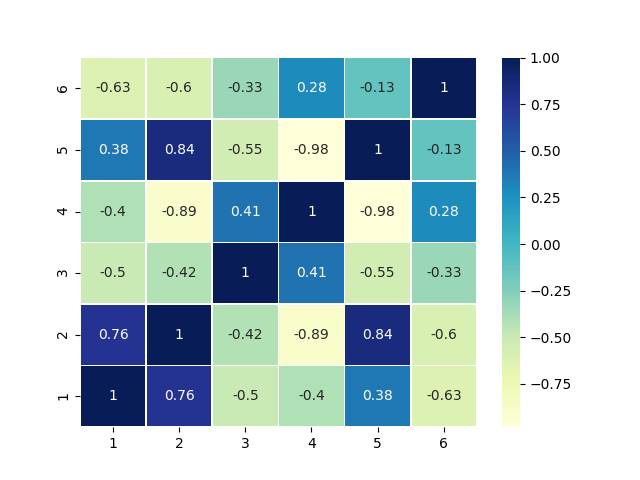
From the above graph, it is clear that the movies Toy Story 1 and Toy Story 2 are very similar. And we can infer this from just their ratings and without any other information!
Another interesting fact to note is that users who liked Toy Story 2 or Jumanji did not like 12 Angry men. This seems likely as the former are children’s movies while the latter is a classic movie meant for adults.
From the graph, we can even start to identify genres - All children’s genres have a positive similarity with each other and a negative similarity with the rest.
The final predictions are:
| Movie 1 | Movie 2 | Movie 3 | Movie 4 | Movie 5 | Movie 6 | |
|---|---|---|---|---|---|---|
| Arthur | 5 | 3.1 | 2 | 1.91 | 3.30 | 1.46 |
Genres
Another thing that I do is explicitly using the genres of each movie. Thus, instead of getting only general recommendations, we can also get genre-specific recommendations. This can be done by masking the rating matrix, i.e. Suppose we need recommendations in the ‘Drama’ genre. We can apply a mask G such that the matrix G*R is zero for all movies that are not in the ‘Drama’ genre.
Movies
To try out what I learned, I played around with the MovieLens database and created a simple Movie recommender system. The dataset consists of 1 million ratings for about 6000 movies.
Usage
The Recommender can be used offline / online. Both versions are compatible, and only the interface is different - the data and algorithms are the same.
Command-line interface
This version is hosted on the master branch of the repository. Follow the installation guide given below. Then use movie.py to get recommendations
1
2
3
4
5
6
7
python3 movie.py [-h] [-s] [-r] [--reset]
optional arguments:
-h, --help show this help message and exit
-s, --search Search for movies by name and rate them
-r, --recommend Let the system recommend movies to you
--reset Remove all of your ratings
Web interface
Navigate to http://movie42-app.herokuapp.com/.
1
2
3
4
5
You can search for movies using the search bar at the top.
There are 3 buttons:
* Recommend - Recommends movies to you based on your ratings (Needs at least 5 ratings for recommendations)
* My movies - Lists the movies that you have rated
* Clear - Clears all ratings so that you can start fresh
Installing locally
This project has 2 interfaces - They are hosted on different branches on the central repository. Although both the versions are very similar and are compatible with each other. It is recommended that you install each one of them in different directories.
Setting up the CLI
Clone the repository Movie-Recommendations and Pull the master branch
1
2
git clone https://github.com/MananSoni42/Movie-recommendations.git
git pull origin master
Install the required dependencies
1
2
apt-get install python3 python3-pip
pip3 instal -r requirements.txt
Download the dataset from here, unzip it and place it in the dataset directory After this, the structure of the dataset directory should be:
1
2
3
4
5
6
7
8
9
├── Movie-recommendations/
└── dataset/
├── dataset.txt
└── ml-1m
├── movies.dat
├── ratings.dat
├── README
└── users.dat
...
Run the following to preprocess the dataset.
1
python3 data_manip.py
This should only take a minute.
Host the server
1
python3 server.py
You are all set up! Visit localhost:5000 and get stellar recommendations!
Setting up the web version
Clone the repository Movie-Recommendations and Pull the web branch
1
2
3
git clone https://github.com/MananSoni42/Movie-recommendations.git
git checkout web
git pull origin web
Install the required dependencies
1
2
apt-get install python3 python3-pip
pip3 instal -r requirements.txt
Note that this requirements.txt is different from the master branch
Now you are ready to process the data. Run the following to preprocess the dataset.
1
python3 data_manip.py
This caches the entire similarity matrix and will take 10-15 minutes to run.
You are all set up! Get stellar recommendations using movie.py
Contributing
Feel free to contribute features / point out errors. Fork my repository and make a pull request.
I promise I’ll have a look!