“ The purpose of computing is insight, not numbers ” - Richard Hamming

What is Numerical Analysis?

Numerical Analysis is an area of Mathematics and Computer Science that is almost as old as computers themselves!
It is concerned with all aspects of the numerical solution of a problem - from the theoretical development and understanding of numerical methods to their practical implementation as reliable and efficient computer programs.
Numerical Algorithms are widely used mainly because the modelling of even moderately complex real-life scenarios leads to equations that have no analytical solutions - we have to rely on approximate numerical methods only.
It naturally finds application in all fields of engineering and the physical sciences, with applications ranging from predicting weather patterns to simulating fluid flow.

About the website

Intended audience

The ideal audience would be undergraduate students that have studied/are studying a course on Numerical Analysis.
This website is built for people who have some basic technical knowledge of the subject but are unable to understand the core material in an intuitive way
It is meant as a visual guide to Numerical Analysis

Goals

The website has been built with three major goals:
- Simplicity and ease of use
- Minimal compromise on the theoretical aspects
- Insightful visualizations
The central goal is to build a website that can assist teachers and students to explain and understand this beautiful subject in a better way.

Organization

The website is organized into six independent, self-contained modules:

Finding zeroes of arbitrary functions
Polynomial interpolation
Numerical differentiation
Numerical integration
Solving linear equations
Solving differential equations

The need for such a tool

Since this tool was a hobby project, it is far from complete and can handle a very limited range of conditions (far too many edge cases have been left out compared to commercially available software), so why use this?

No need to learn any syntax

Most of the other Numerical Analysis tools out there require their users to know the syntax of the tools
This is a hassle for most beginners
In comparison, this tool requires no syntax knowledge

Focus on simplicity and interactive design

Most existing solutions, tend to focus more on efficiency rather than simplicity (as they are not designed for students)
This tool has been thoughtfully designed so that it can be used to interactively while teaching the subject as well as later on to explore
This tool has also been successfully tested in the Numerical Analysis course (2020 sem-I) at BITS Pilani, Pilani campus

Usage & Examples

The examples presented show the intended use of the website.
They are present in a question-answer format (as this is the most common use case).

Q1 - Finding zeroes - I

Find a zero of the function \((x-3)(x+7)\) given that there is a zero in the interval (-1,10)

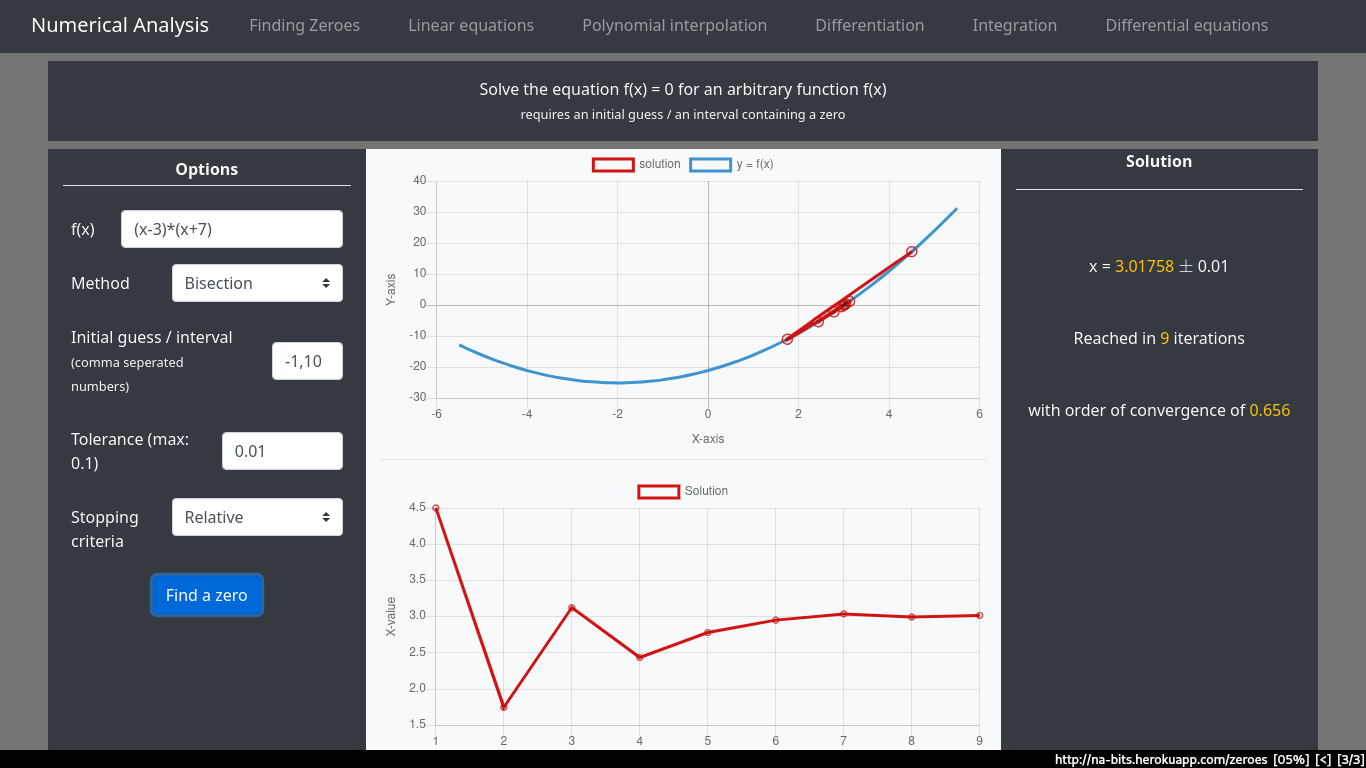
zero-bisection

Solution using the bisection method, with an initial interval of (-1,10) We can see that the order of convergence is quite low for this method, meaning this particular algorithm converges very slowly

Q2 - Finding zeroes - II

Find the zero closest to 100 of the function \((x-3)(x+7)\)

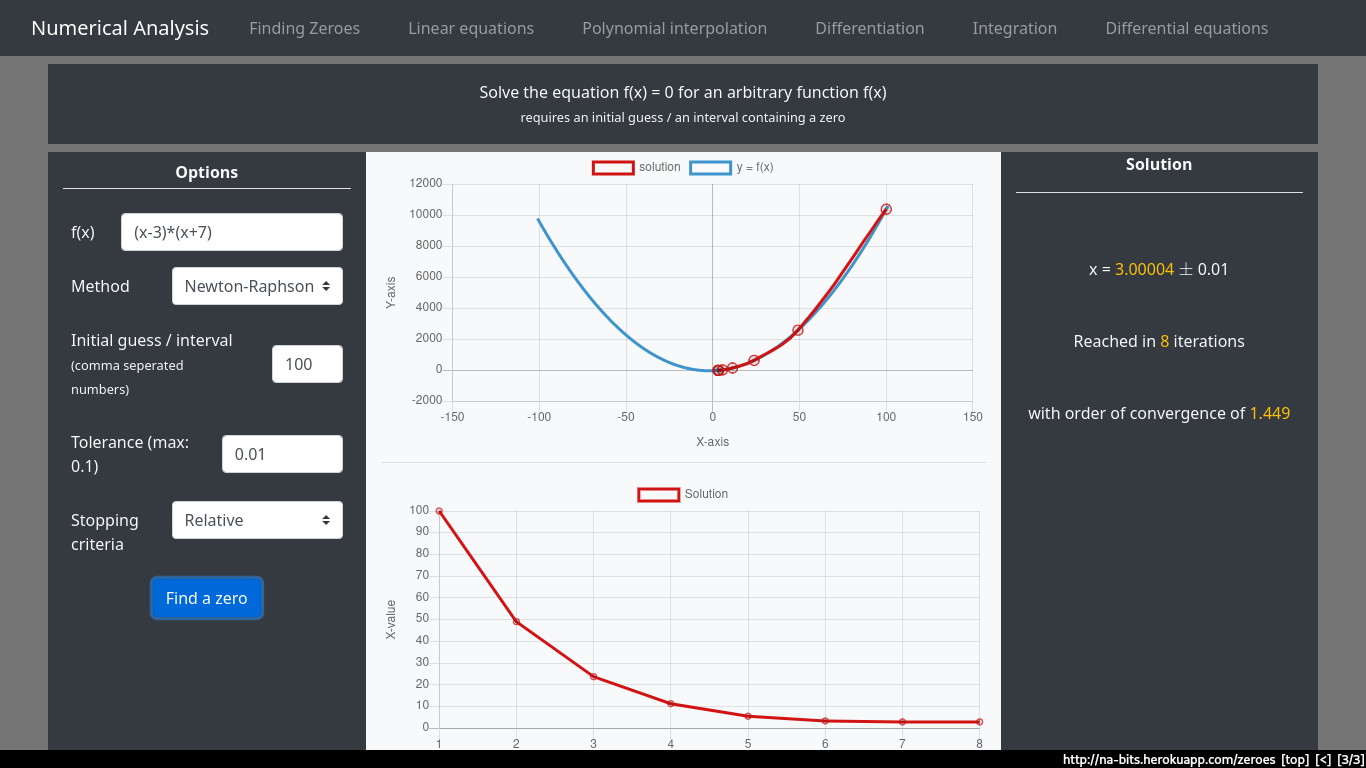
zero-newton

Solution using Newton’s method, with an initial guess of 100.
We can see that the order of convergence is much better, in fact, newton’s method is widely used due to its relative simplicity and high order of convergence

Fun fact: The legendary fast inverse square root is just computing 2 iterations of newton’s method (in hexadecimal)

Q3 - Numerical integration

Integrate \((x-4)x(x-5)\) from -5 to 7

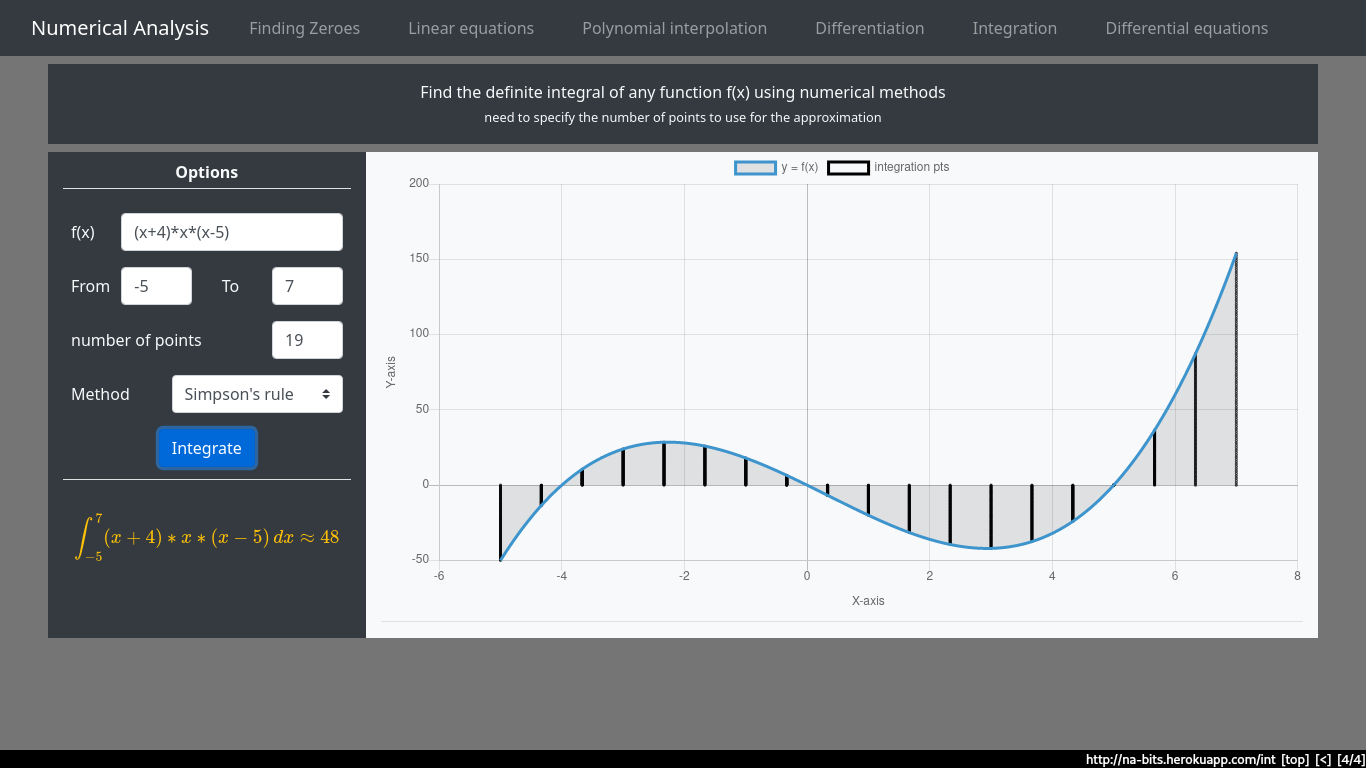
int-simpsons

Solving using the easiest method - Simpson’s rule. The Simpsons rule uses equally spaced points to approximate the interval

Fun fact: Scientific calculators generally use (a modified version of) the Simpsons rule to calculate definite integrals

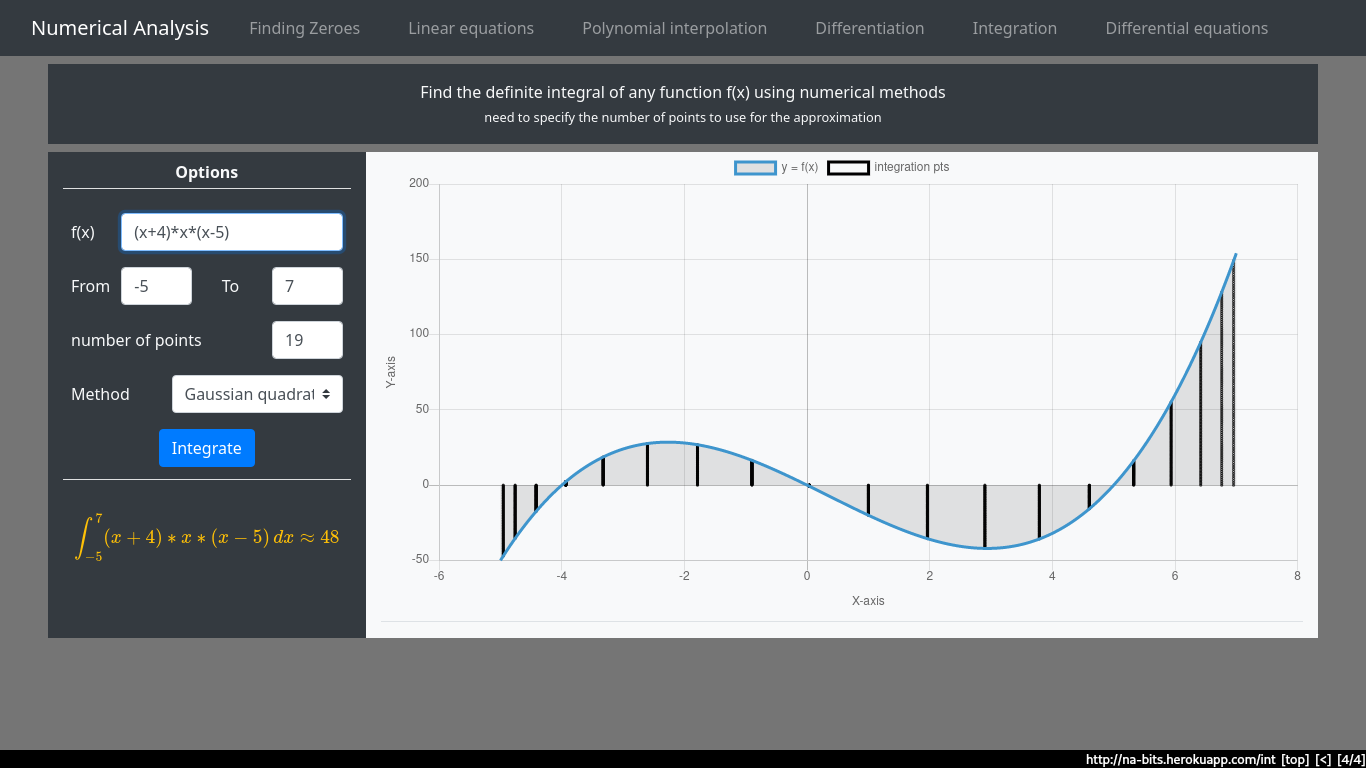
int-quadrature

Solving using the best available method - Gaussian quadrature. As you can see, Gaussian Quadrature uses unequally spaced points - it optimizes the positions of these points to minimize the approximation error.

Q4 - Interpolating data points

Interpolation: TODO

Q5 - Solving Differential eqns

What is the solution of the linear first order differential equation: \(y' = - 15 y\) 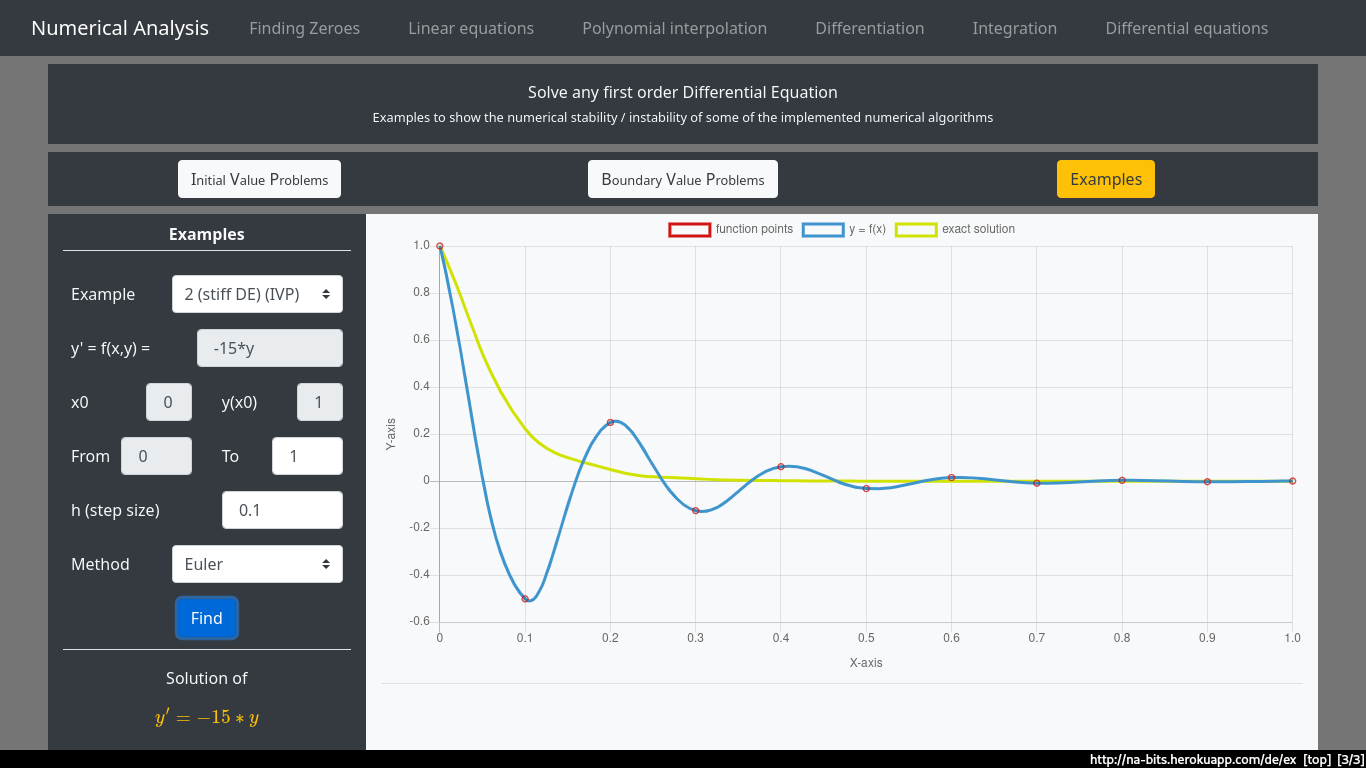de-euler

Solution using the simplest available method - Eulaer’s method. We can clearly see that the approximate solution oscillates about the exact solution instead of converging

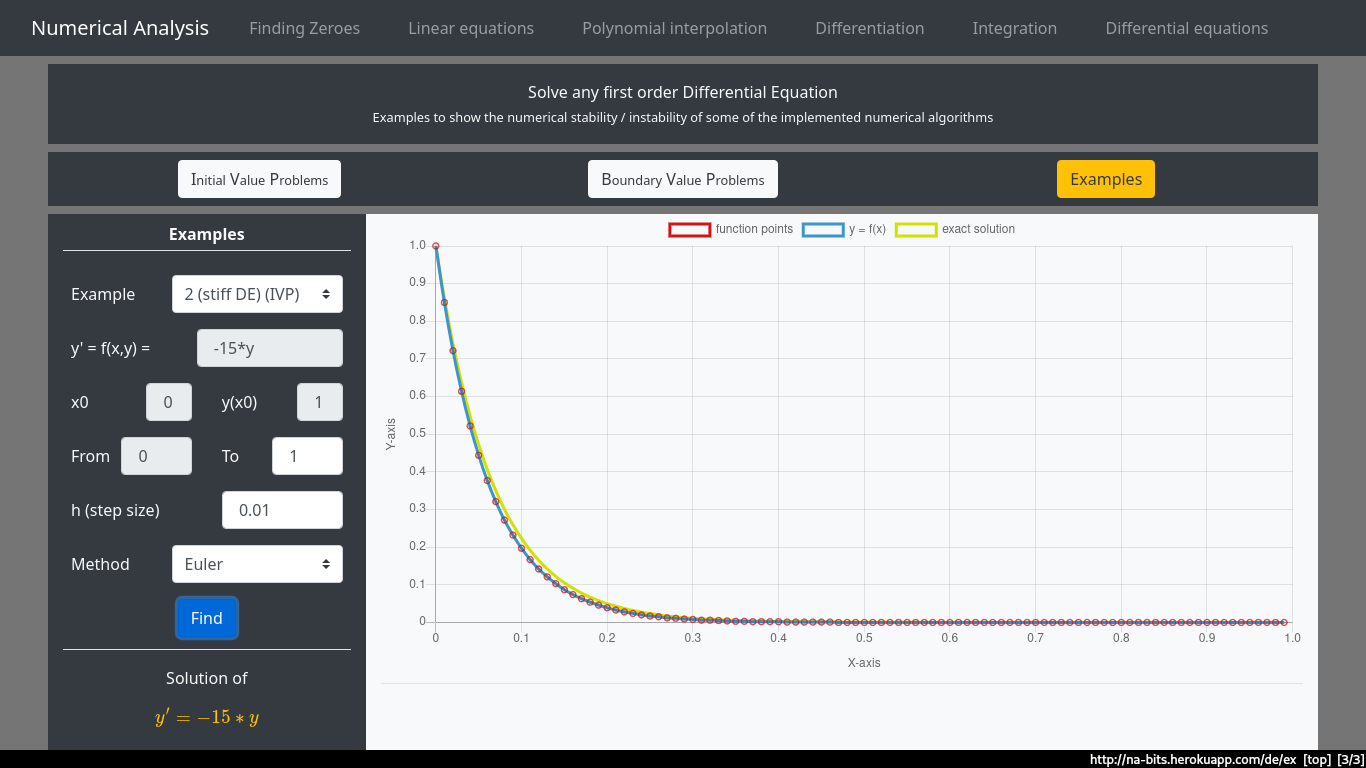
de-euler-2

We can lower the step size (h) to get a better approximation (in fact, we can prove that for any differential equation, these single-step methods converge to the exact solution for a )